- 1 : 2022/04/10(日) 20:54:21.184 ID:8thijowT0
- 2 : 2022/04/10(日) 20:54:42.480 ID:8thijowT0
-
あげ
- 3 : 2022/04/10(日) 20:55:02.179 ID:8thijowT0
-
あっげあげ
- 4 : 2022/04/10(日) 20:55:07.780 ID:EYLtailTr
-
計算するとそうなる
- 6 : 2022/04/10(日) 20:55:40.772 ID:WaQGVkJRa
-
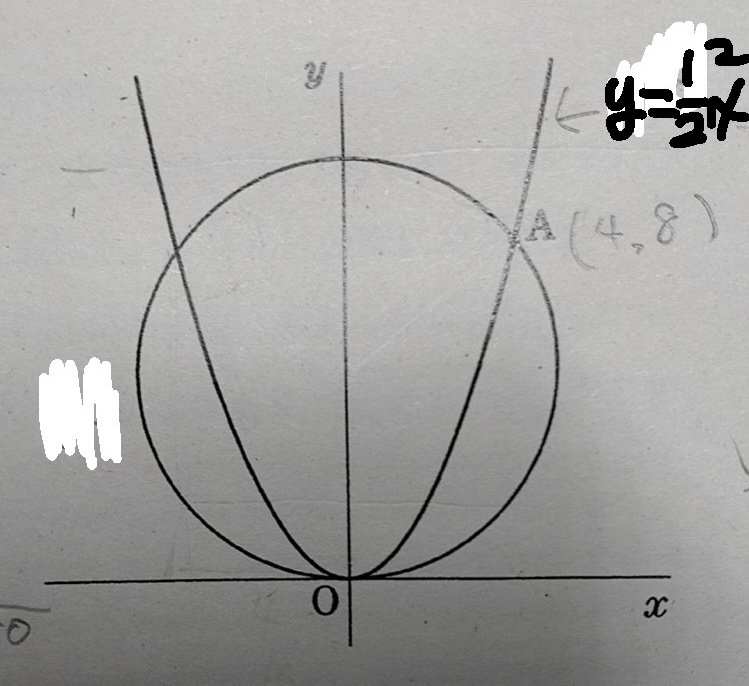
(0,0)(4,8)(-4,8)を通る円
- 8 : 2022/04/10(日) 20:56:05.731 ID:8thijowT0
-
>>6
うん。? - 10 : 2022/04/10(日) 20:56:37.937 ID:ujGpcVSL0
-
>>8
それを代入 - 13 : 2022/04/10(日) 20:57:33.235 ID:8thijowT0
-
>>10
何に代入するの? - 39 : 2022/04/10(日) 21:03:30.136 ID:azTkHTkJ0
-
>>6で終わったスレ
- 7 : 2022/04/10(日) 20:55:45.329 ID:8thijowT0
-
(^ω^)あぶらあげ
- 9 : 2022/04/10(日) 20:56:17.091 ID:yTZZBY5X0
-
放物線の内側の線を消してみ?
おちんちんみたいだから - 11 : 2022/04/10(日) 20:56:46.816 ID:8thijowT0
-
VIPに数学強い人いないのか?
- 12 : 2022/04/10(日) 20:57:25.234 ID:TOYjTUq50
-
これがわかる程度で数学が強いのか?
- 15 : 2022/04/10(日) 20:58:05.516 ID:8thijowT0
-
>>12
すまん、俺が弱いだけだわ。 - 14 : 2022/04/10(日) 20:58:00.770 ID:of1euG+00
-
0,0
4,8
0,u
を通る円じゃねえの? - 17 : 2022/04/10(日) 20:58:43.803 ID:8thijowT0
-
>>14
それがよく分からない。。。 - 31 : 2022/04/10(日) 21:01:35.183 ID:of1euG+00
-
>>17
は?
円の方程式はパラメータが3つだから独立した3点があればパラメータ全部決定するだろ?直線が2点与えられれば直線の傾きとy切片がわかるのと同じだぞ?
- 16 : 2022/04/10(日) 20:58:32.339 ID:Tjcaw/NnH
-
(x-a)^2+(y-b)^2=r^2
って公式知ってる? - 19 : 2022/04/10(日) 20:59:07.461 ID:8thijowT0
-
>>16
え、知らね - 18 : 2022/04/10(日) 20:58:47.304 ID:766aK+oW0
-
変な補助線引いてて笑う
- 21 : 2022/04/10(日) 20:59:22.621 ID:8thijowT0
-
>>18
気にするな。 - 20 : 2022/04/10(日) 20:59:15.832 ID:OscEWefMM
-
Oと(4,8)を通る以外の条件はあるの?
- 24 : 2022/04/10(日) 20:59:47.737 ID:8thijowT0
-
>>20
これ以上にヒントは無い。 - 26 : 2022/04/10(日) 21:00:42.102 ID:OscEWefMM
-
>>24
じゃあ中心は無限にある - 22 : 2022/04/10(日) 20:59:39.276 ID:Si8iBxfN0
-
OAの垂直二等分線とy軸の交点
- 23 : 2022/04/10(日) 20:59:47.600 ID:Nd8n8vmS0
-
円の中心を(t、0)とすると
円の方程式は
(x-t)^2+y^2=t^2とおける
これにAを代入してtについて解けばOK - 27 : 2022/04/10(日) 21:00:48.280 ID:Nd8n8vmS0
-
>>23
すまん(0、t)
xとy座標逆にしてる - 33 : 2022/04/10(日) 21:02:09.604 ID:Nd8n8vmS0
-
>>23
正しくは
x^2+(y-t)^2=t^2 - 25 : 2022/04/10(日) 21:00:12.964 ID:rWKPJzzF0
-
半径rとすると中心(0,r)だから
(x-r)^2+(y-r)^2=r^2
y軸対称のグラフだから(4,8)を通るなら(-4,8)も通る
だから(x,y)に(0,0),(4,8),(-4,8)代入して連立方程式解く - 28 : 2022/04/10(日) 21:00:59.701 ID:rWKPJzzF0
-
>>25
間違えた
x^2な - 29 : 2022/04/10(日) 21:01:08.400 ID:3hUm74Qea
-
円の中心の座標を(0,a)とすると
三平方の定理から4^2+(8-a)^2=a^2
これを解けばいい - 30 : 2022/04/10(日) 21:01:23.884 ID:rdk5UP/Q0
-
相似とさん平方で溶けそう
- 34 : 2022/04/10(日) 21:02:10.494 ID:3hUm74Qea
-
円の方程式習ってない可能性あるだろ
- 35 : 2022/04/10(日) 21:02:16.463 ID:sAlZpCXe0
-
てす
- 36 : 2022/04/10(日) 21:02:16.888 ID:kDF1CKQO0
-
x^2+(y-r)^2=r^2
ここにx=4 y=8 を代入したら半径出るから終わり - 37 : 2022/04/10(日) 21:02:23.306 ID:qRdbN3Jdd
-
ある点Pの座標が(a,b)とすると、座標平面上で(x-a)^2+(y-b)^2=r^2の方程式を満たす点(x,y)の集合は、点Pを中心とした半径rの円となる
- 38 : 2022/04/10(日) 21:02:53.875 ID:qRdbN3Jdd
-
>>37
なぜそうなるかというと、三平方の定理を用いる - 40 : 2022/04/10(日) 21:04:09.362 ID:8thijowT0
-
ありがとう、解いてみる。
- 41 : 2022/04/10(日) 21:06:11.929 ID:kDF1CKQO0
-
これ中学分野じゃ流石に解けないか
円の方程式使わないとして余弦定理使う解法しか思いつかん
【数学】誰かこの問題解いて



コメント