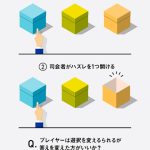
-
確率がわかる人と実はわかっていない人の決定差
https://toyokeizai.net/articles/-/602465 -
答え：
変えた方がいい
確率が倍になるから -
>>2
1/3*2=1/2…ってコト！？ -
選ばれていない方が持っている確率が集約されるので変えた方がいいわけ
-
司会者が当たりの箱を知っているか否かで心理戦に突入する
-
解けるってなに？
-
モンティパイソンなら解いたわ
-
経験上、変えない方がよい
-
>>8
これ -
>>8
これ
100回この問題繰り返すのなら解るけど
自分が挑戦出来るのはこの一回限りでどのみちただの2択なんだよな -
変えて間違った時の方が心理的ショック大きそう🥺
-
逆に考えるんだ
選んでない方の2つを選んでるんだってね -
ドア100個にして考え直すとすぐわかる
-
>>1
1枚目は微妙なところで2枚目は間違いなく設題を簡易に示そうとして失敗しているなだって『挑戦者がより当たりの高くなる行動を取るべきである』って前提は外野の思い込みとしては存在しても設題として与えられてはいないからな
-
変える変えないって聞かれること自体が確率二分の一になる感が出て間違えるよな
100個にしても分からない言う人はここで詰まってると思う。 -
たぶん司会者の顔に出てるｗ
-
この手の問題が理解できない人は、後出しの情報で確率が変動することが分かってないやつ
トランプのダイヤ3枚のやつも「日本語の問題」とか「捉え方の差で変わる」とか言っちゃうやつと同じ -
これ直感的に考えると確率は変わらないって思うわけだけど、実は違うって話だよねw
-
そんな状況は無い
馬鹿な事言ってねえで働け -
司会者が当たりの位置知っているという前提だから顔面でも観察してた方が当たるぞ
-
変えなかったら正解する確率は1/3
変えた場合は最初の選択が間違っていた場合に正解するから正解する確率は2/3
簡単じゃん -
1回目の三択で外れ選んでいれば勝ち
-
最初の箱をキープした場合は、あたりを引ける確率は三分の一で変わらないが、選択を変えた場合は三分の二の可能性で当たりをひけるわけであるねつまりw
-
全部開けるし全部もらう
暴力は確率を凌駕する -
最初に持ってた確率は維持されるからね(´・ω・｀)
-
この問題を真に数学的に理解してるかどうかは「司会者が正解の扉を知っている場合と知らない場合で異なる結論になるか否か」の問いに対して計算プロセス含めて正しく答えられるかでわかる
-
100個にして考えるとわかるだろ
1/100を選ぶか1/2を選ぶかどっちってことじゃん -
場合をすべて示すとこうなります
はい変えた方が倍になりますね1に商品がある場合
1を選ぶ → 変更しない-Win .変更する-Lose
2を選ぶ → 変更しない-Lose 変更する-Win
3を選ぶ → 変更しない-Lose 変更する-Win2に商品がある場合
1を選ぶ → 変更しない-Lose 変更する-Win
2を選ぶ → 変更しない-Win .変更する-Lose
3を選ぶ → 変更しない-Lose 変更する-Win3に商品がある場合
1を選ぶ → 変更しない-Lose 変更する-Win
2を選ぶ → 変更しない-Lose 変更する-Win
3を選ぶ → 変更しない-Win .変更する-Lose -
>>27
総当たりで書き出すだけでわかるのに数学者も引っかかったらしいから面白いよなー -
つまり選択をかえた場合、ハズレを引く可能性は最初にキープした箱にあたりが入ってた場合だけで、その可能性はやはり三分の一。
つまり三分の一しかハズレの可能性ないということは、論理必然的にあたりの可能性は三分の二となるわけであるねw
-
NHKの笑わない数学でやってたな
実際に検証を繰り返していったら変えた方が当たるって結論になった -
最近知ったのか？
-
モンティ・ホール問題のスレは以前にもたぶん何回かたってたよね嫌儲にw
【テスト】まさかモンティホール問題も解けないのにエラソーに語ってるやつなんて嫌儲にはいないよね？
コメント